Головна | Заняття | Консультації

Консультації для вихователів

Чи готовий ваш дитина до школи?

Пропонуємо Вам роботу чудових педагогів Венгер Л. А., Марциковской Т. Д., Венгер А. Л., присвячених специфіці старшого дошкільного віку.

Більше, менше, порівну

Ваша дитина вже оволоділа початковими уявленнями про кількість. Він вміє рахувати, знайомий з числовим рядом в межах 10, знає цифри. Будемо виходити з того, що, користуючись нашими порадами з попередньої книжки, ви познайомили його з поділом цілого на рівні частини, показали, що ціле завжди більше своїх частин, і, якщо розділити ціле на частини, то з них знову можна зібрати ціле.

Тепер уявлення про співвідношення цілого і частин може бути використано в якості основи для навчання рішенню елементарних арифметичних завдань.

На перший погляд задачі на додавання і віднімання в межах першого десятка досить прості. Якщо дитина знає склад числа і вміє рахувати, їх рішення не повинно представляти ніяких труднощів. Але таке враження оманливе. Воно відразу ж зникне, як тільки ви спробуєте задати кілька завдань.

- На дереві сиділо 4 пташки. Прилетіла ще 1. Скільки стало пташок?

- У тебе було 5 цукерок, 2 ти з'їв. Скільки залишилося?

- На тарілці лежали яблука. 2 мама віддала дітям. Залишилося 4. Скільки було яблук?

- На дереві сиділи пташки. Потім прилетіли ще 3 пташки, і їх стало 5. Скільки пташок спочатку було на дереві?

Можливо, що перші дві задачки ваша дитина вирішить правильно. А ось третю і четверту - навряд чи. В чому справа? Яка різниця? Різниця є, і дуже значна.

Ви починаєте ставити умови першої задачі. "На дереві сиділо 4 пташки". Дитина уявляє собі дерево, пташок, що сидять на ньому. Або (якщо кількість для нього вже досить відокремлено від самих предметів) просто чотири фішки, кісточки на рахунках. Можливо, він загинає 4 пальця. Нарешті, не виключено, що йому досить запам'ятати число 4 у вигляді цифри. "Прилетіла ще 1", - ви продовжуєте. Одразу ж ясно, що сталося: до чотирьох додалася одиниця. Про це свідчить саме слово "прилетіла". Її можна уявити собі у вигляді додаткової пташки чи фішки, загнути ще один палець і перерахувати їх загальна кількість або просто згадати, що в числовому ряду після чотирьох йде п'ять.

Ненабагато складніше і друге завдання. Тут теж саме слово "з'їв" свідчить про зменшення, зникнення якогось кількості. І теж все легко порахувати на пальцях або в розумі. Для 5 цукерок загинаються 5 пальців, потім 2 з них розгинаються. Залишилися перераховуються. Або по числовому ряду йде відлік: "п'ять, чотири, три".

Зовсім інша справа - третя завдання. Тут уявляти собі лежать на тарілці яблука неможливо - адже не сказано, скільки їх. З тієї ж причини не можна загинати пальці. Перше число, що з'являється в задачі, - 2. "Віддала 2". Але "віддала" - це означає, кількість зменшилася. Треба віднімати. А від чого забирати? "Залишилося 4". Мабуть, саме природне спонукання в цьому випадку від 4 відняти 2.

Того ж роду труднощі виникають перед дитиною і при рішенні останньої задачі. Завдання, подібні першим двом, називаються "прямими", а подібні двом останнім - "непрямими". Зазвичай їх рішення погано дається навіть учнів 2-3-х класів. Звичайно, там вводяться великі числа. Але справа не в числах. Навіть у випадках, коли молодші школярі знаходять правильне рішення, вони часто не можуть пояснити, як його отримали. Непрямі завдання - прекрасний матеріал для перевірки того, наскільки дитина навчився розбиратися в будь-яких завданнях, розуміти їх математичний сенс.

Для того щоб допомогти дитині прийти до такого розуміння, фахівці пропонують різні прийоми. Найбільш вдалий, на наш погляд, той, який розробила для дошкільнят психолог Н.І.Непомняща. Він якраз і базується на використанні уявлень про співвідношення цілого і частин.

Що таке ціле і що таке частині, дитина вже знає. Але якщо не знає - не біда. Це не так-то складно пояснити. Ось листок паперу. Якщо його скласти і розрізати чи розірвати, вийде дві частини. А якщо ці частини скласти і склеїти, знову вийде ціле. Листок можна розрізати в різних місцях. Залежно від цього частини будуть виходити різні. Вони можуть бути однаковими (рівними), а можуть бути і нерівними (це потрібно підкреслити спеціально, якщо раніше ви знайомили дитини тільки з поділом цілого на рівні частини). Частин може бути дві, а може бути, і більше, але ціле вийде, тільки якщо зібрати разом всі частини, скільки їх є.

Найважче для дитячого розуміння - відносність понять "ціле" і "частина". Будь-яка величина може бути в одному випадку цілим, в іншому - частиною.

Ви ставите на стіл три склянки. Один з них повний, два порожніх.

- Дивися, Мишко. В цьому стакані - вода. Вся вода, яка в нас зараз є. Це ціле чи частина?

- Ціле.

- Звичайно. Давай покладемо сюди цілу паперову смужку, щоб пам'ятати, що це ціле. А тепер розіллємо воду з двох склянках. В кожній склянці буде частина води. Як це показати на смужці?

- Розірвати її (смужка розривається на дві частини і кожна підкладається до одного з склянок з водою).

- Як ти думаєш, вода в цьому стакані (одного з двох) може бути цілим?

- Ні, адже це частина!

Один із склянок з водою прибирається. Прибирається і відповідна йому частину смужки.

- А тепер?

- Тепер це ціле, тому що більше води немає.

- Правильно. А це ціле можна розділити на частини?

- Так. Потрібно відлити в порожній стакан.

- Вірно. Покажи це на смужці, потім отлей (смужка, яка раніше означала частина, тепер розривається на дві, її частини підкладаються до двох склянках, потім частина води переливається в порожній стакан).

- А як знову зробити з частин ціле?

- Злити воду разом.

Такі ж паперові смужки послужать моделлю відносин частина - ціле і коли цілим є окремий предмет (наприклад, намальована автомашина, яку можна розрізати на частини і знову скласти), і коли це - сукупність предметів. Останній випадок особливо важливий для подальшого навчання рішенню завдань.

На столі 8 олівців, складених у купку. Знову береться паперова смужка.

- Ці олівці - частина чи ціле?

- Ціле, тому що інших олівців тут немає.

- Так, це ціле. Всі ці олівці і буде позначати смужка.

Ви ділите олівці на дві групи (4 і 4 або 5 і 3).

- Що я зробив з цілим?

- Розділив його на частини.

- Давай покажемо це на смужці (смужка розривається на дві, і кожна частина підкладається до групи олівців).

- А як показати на смужці, що ми знову хочемо з'єднати всі олівці, зробити з частин ціле?

Кожен раз розривати і склеювати смужку занадто клопітно. Її можна замінити іншими позначеннями.

- Тепер ми будемо позначати ціле гуртком, а будь - половинкою гуртка.

Дайте ще кілька завдань з поділом цілого на частини і об'єднанням частин. При цьому нехай дитина, "вгадуючи", де ціле, де частини, прикладає до цілого гурток, до частин - половинки гуртка (вони заздалегідь вырезываются з паперу або картону).

- Міша, я покажу тобі, як можна без слів дізнатися, що ми хочемо зробити: ціле з частин або частини цілого. Це буде ніби зашифрована команда. Ось такий значок (він називається плюс) означає, що частини з'єднуються, а такий значок (він називається мінус) від цілого віднімають частина.

Значки "+" і "-" малюються на окремих картках і показуються дитині в ході пояснення.

- Ось лежать 2 кубика, а тут ще 2. Я даю тобі таку команду.

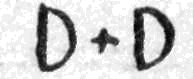
("Команда" викладається з трьох відповідних карток).

Як ти думаєш, що ти повинен зробити? Правильно, з'єднати їх разом. А якщо команда буде така.

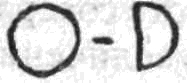
Так, від всіх кубиків потрібно відняти частину. Скільки хочеш.

- А тепер ти давай мені команди і дивись, чи правильно я їх виконую.

Пора переходити до завдань.

Ви даєте дитині 3 олівця, потім ще 2. Нехай він розповість, що ви зробили. Допоможіть докладного оповідання з позначенням кількості. Не просто: "Ти дав мені олівці", а "Ти дав мені спочатку три олівця, а потім ще два". Після цього дитина повинна здогадатися, яке запитання можна поставити. В даному випадку це питання: "Скільки стало олівців?" Тепер потрібно записати те, що сталося. Запропонуйте дитині відразу викласти умови завдання з цифр і знаків (вони беруться з каси цифр).

Те ж саме відноситься і до завдань, що передбачають дію віднімання. У дитини 6 кубиків. Ви забираєте один з них і допомагаєте скласти задачу: "У мене було 6 кубиків, 1 ти забрав. Скільки залишилося кубиків?" Якщо дитина не може, завдання складаєте ви самі: "У тебе було 6 кубиків, 1 я забрав. Скільки кубиків у тебе залишилося?" Завдання записується у вигляді числового прикладу: 6 - 1 = і вирішується.

Наступний крок завдання, які ви задаєте самі на наочному матеріалі. "Я поклав на стіл 2 вилки, а потім ще 2. Скільки стало вилок?" Дитина записує завдання у вигляді числового прикладу і вирішує її.

Від ситуацій, які виникають на очах у дитини, переходите до ситуацій, в яких описуються ті чи інші події. На перших порах до них можна давати наочні ілюстрації. "В будиночку жили 5 сестричок (на стіл ставиться 5 матрьошок), дві з них пішли гуляти (дві матрьошки прибираються). Скільки сестричок залишилося в будиночку?"

А потім можна буде обходитися і без ілюстрацій - ставити завдання усно.

"У дівчинки було 4 яблука. Їй дали ще 2. Скільки у неї стало яблук?"

"У хлопчика було 7 олівців. Він втратив 3. Скільки у нього залишилося олівців?"

Такі завдання - найлегші. Це вже знайомі вам "прямі" завдання. В них дії розгортаються послідовно, а в самому тексті містяться слова, що вказують, що відбулося - збільшення чи зменшення початкової кількості.

Більш важкими можуть виявитися для дитини завдання, де немає слів, що позначають дію: "У кошику було 5 підберезників і 3 подосиновика. Скільки грибів було в кошику?"

Але ще важче, звичайно, "непрямі" завдання, де послідовність опису умов не збігається з послідовністю ходу рішення.

Тут-то і знадобляться засвоєні дитиною уявлення про співвідношення цілого і частин. Будь-яку задачу можна зрозуміти і вирішити, якщо встановити, де в ній зазначені частини, а де ціле, що залишилося невідомим.

"Мама купила 7 цукерок. Миколка з'їв дещо і залишив 3 цукерки. Скільки цукерок він з'їв?"

Що сказано в цій задачі? Сказано, скільки всього було цукерок? Так, їх було 7. Це ціле. Миколка з'їв всі цукерки? Ні, не всі. Значить, Миколка з'їв частину цукерок, але ми не знаємо, скільки. А залишилися всі цукерки? Ні, теж частина, і ми знаємо, що в цій частині було 3 цукерки. Але якщо ми знаємо і одну з частин, як можна дізнатися іншу частину?

"На столі лежали книжки. Потім поклали ще 3 і стало 5. Скільки книжок лежало спочатку?"

Де тут частині, а де ціле? Спочатку на столі лежали всі книги чи ні? Немає. Лежала тільки частина книг, тому що потім принесли ще і книг стало більше. Значить, принесли ще частина вийшло ціле. Про це ціле ми знаємо, що в ньому було 5 книг, а про частину, яку принесли, що в ній було 3 книги. А не знаємо ми, скільки книжок було в тій частині, яка лежала на столі раніше. Як це можна дізнатися?

Наводячи приклади подібних міркувань, ми зовсім не маємо на увазі, що їх повинен повторювати для дитини дорослий. Це нічого не дасть. Так, в остаточному підсумку повинен навчитися міркувати сам дитина, а роль дорослого полягає в тому, щоб підводити його до цього. Але якщо дитина навчився міркувати подібним чином стосовно до будь-яких типів завдань в одну дію - мета досягнута: він опанував розумінням математичного змісту текстових задач, за яких лежить відношення " ціле - частина.

А тепер ми хочемо коротко нагадати деякі види завдань, найбільш корисні для розумового розвитку шестирічної дитини, - на той випадок, якщо у вас немає книжки "Домашня школа".

У сюжетно-рольовій грі дитина практично освоює відносини між людьми. Взявши на себе яку-небудь роль, він навчається поводитися відповідно з цією роллю ("вчителі", "учня", "матроса", "капітана" і т. п.).

Щоб підвищити розвиваюче значення гри, потрібно допомагати дитині будувати різноманітні сюжети, привчати його міняти свою роль по ходу гри (виконуючи, таким чином, дві або більше ролі поспіль). Граючи з дитиною, намагайтеся будувати ситуації, в яких найбільш яскраво проявляються взаємовідносини людей, розподіл функцій між ними. Задум гри корисно намітити з дитиною заздалегідь, але лише в самому загальному вигляді, щоб замість живої імпровізації не вийшло розігрування готового сценарію.

Ігри-драматизації, наближаються до гри акторів на сцені і розгортаються за суворим сценарієм (взятим із знайомої казки або розробленого вами удвох з дитиною), теж корисні старшим дошкільнятам. Але все ж їх значення для розвитку уяви, самостійності, творчих можливостей істотно поступається значенням вільної сюжетно-рольової гри.

Нагадаємо і про режисерських іграх, в яких дитина "роздає ролі" лялькам, іграшковим звірам, олов'яним солдатикам і т. п. Зрозуміло, "оживляти" всіх цих персонажів доводиться йому самому - на перших порах разом з мамою або татом. Керуючи своїми "артистами", він може будувати складні оригінальні сюжети. Значна частина сюжету "програється в умі", з іграшками відбуваються лише окремі дії. Такі ігри сприяють розвитку уявного планування дій, формують уміння уявляти собі різноманітні складні ситуації, наслідки своїх вчинків.

Багатющі можливості для розвитку дитини надає дитяча література. У попередніх книжках ми рекомендували поряд з читанням дитині казок і віршів проводити спеціальну роботу по навчанню їх "розігрування" з заступниками, переказу, "досочинению", самостійного твору.

Для "розігрування" казок вам знадобляться паперові гуртки або квадратики різного кольору і різної величини - вони будуть зображати персонажів казки. З їх допомогою зручно відображати дії героїв. От вовк зустрівся з лисицею - дитина підносить сірий гурток до помаранчевого. А ось лисиця побігла по своїх справах - помаранчевий гурток відкладається в сторону. Таке "розігрування" дитина може проводити під час читання казки дорослим, а може потім з його допомогою "показати" казку, супроводжуючи дії розповіддю. Якщо замалювати розташування заступників, які відповідають основним епізодів казки (так, щоб вийшла серія малюнків), то вийде її схематичний конспект, дивлячись на який дитина згодом легко зможе пригадати і переказати зміст прочитаного.

Опорою для переказу може служити і послідовність звичайних (але досить простих і умовних) малюнків - зроблених дитиною ілюстрацій до голів, на які ви разом з ним розбиваєте казку. Кожній главі дитина дає назву, і в результаті виходить більш або менш докладний план.

Для розвитку уваги до художньої формі ми рекомендували гру "Чуже слово". Вона буде корисна і шестирічним дітям. Гра проводиться так. Ви читаєте дитині незнайоме йому вірш, замінивши в ньому одне слово. Спочатку проводяться грубі заміни: вставляється слово, яке не відповідає ні за змістом, ні ритму, ні за римі. Незабаром дитина навчиться легко знаходити слово, яке "не встало на своє місце", і підбирати замість нього більш підходяще (можливо, в цьому йому треба буде допомогти). Тоді можна переходити до більш тонким замін: вставляти слова, що підходять за змістом, але вибиваються з ритму або порушують риму.

Деякі шестирічні діти вже вміють читати самостійно. Не думайте, що в цьому випадку можна перестати читати дитині вголос. Це різко збіднить його знайомство з художньою літературою, знизить рівень її розуміння. При самостійної роботи дитини над книгою майже всі його увага йде на сам процес читання, з-за цього зміст прочитаного від нього часто вислизає.

Щоб дитина не звикав читати, не розуміючи прочитаного, давайте йому для самостійного читання тільки простий короткий текст, бажано з численними ілюстраціями, пояснювальними його сенс.

Для розумового розвитку шестирічної дитини, як і для розвитку дітей 3-5 років, дуже корисна образотворча діяльність. Намагайтеся домагатися різноманітності сюжетів, втілюваних у малюнках і пластилінових скульптурах вашої дитини. Обговорюйте з ним задум, пропонуйте нові цікаві для нього теми: "Намалюй, як ти будеш вчитися в школі"; "Вылепи циркових артистів - наїзницю, клоуна, гімнастів" і т. п. При плануванні малюнка корисно заздалегідь намічати місце, відведене для кожного зображення задуманого об'єкта, вказуючи рукою або обводячи легкої олівцевої лінії. Частіше звертайте увагу дитини на позу зображуваного персонажа (скажімо, якщо людина сидить, то ноги у нього повинні бути зігнуті).

І нарешті, кілька слів про роботі з будівельним матеріалом. З шестирічною дитиною потрібно продовжувати заняття конструюванням з різних видів зразків. Особливо корисно конструювання за нерасчлененному кресленням (на якому зображена форма заданої споруди, але не зображено її членування на будівельні деталі) і з суто умовного схематическому зразком, лише приблизно заданому тип необхідного споруди.

Нерасчлененный креслення зображує вид споруди з якої-небудь певної позиції. Корисно поєднувати два таких зразка, на одному з яких зображений вид збоку, на іншому - вигляд спереду або зверху.

Ми не даємо порад щодо навчання дітей грамоті, так як переважна більшість шестирічних дітей навчається їй у школі або в дитячому садку. Якщо домашнє навчання прийде в протиріччя зі шкільним або дитсадкових (за методами, темпами тощо), то воно може виявитися корисним, а шкідливим. Не можна виробляти один і той же навик (в даному випадку навичка читання) двома різними методами одночасно.

А як же математика? Адже її теж вчать в дитячому саду і в школі! Вірно. Але в цьому випадку мова йде не про вироблення конкретної навички, а про розвиток уявлень певного роду (уявлень про кількісних відносинах об'єктів). Тут цілком можна поєднати два різних підходи - математичні вистави від цього не постраждають, а тільки збагатяться.

Матеріали, розміщені на сайті, надіслані користувачами, взяті з відкритих джерел і представлені на сайті для ознайомлення. Всі авторські права на матеріали належать їх законним авторам. Використання матеріалів дозволено тільки з письмового дозволу адміністрації сайту.
При копіюванні матеріалів пряме посилання на сайт обов'язкове